南京紫东江宁学校（初中）数学备课组活动

一、情况概述

2020年9月4日，邵凤君老师执教七年级上册《有理数与无理数》，这是本学期第一次集体备课。本次备课主要围绕“常规课堂，素养提升”这一主题进行教学设计。

二、活动方案

1.活动时间

听课：2020年9月4日上午第三节 研讨：上午第四节

2.活动地点

听课：七年级（一）班教室

研讨：初中部办公室

3.活动主题

常规课堂，素养提升

4.活动目的

为每位老师搭建展示和交流的平台，营造浓浓的教研氛围，有效地促进教师专业成长。此次备课活动，是数学备课组常态化的备课活动，希望通过这样的活动，教师关注并激活如下课堂教学要素：问题情境、合作探究、倾听与对话、交流与展示，催生指向“核心素养”的教与学。教师是教学的源头活水，他应在课堂中与学生共同成长，获得成就与尊严。

5.活动步骤

①组长提前一天发活动通知，本组教师提前熟悉教材。

②邵凤君老师在七年级（一）班执教《有理数与无理数》，全体数学教师听课学习。

③在初中办公室开展教学探讨，各备课组教师代表整理自己的想法依次发言。

④主持人归纳总结。

6.活动要求

每位数学教师根据通知提前参阅相关教学资料，熟悉本次活动的听课内容及研讨主题，围绕主题准备自己的发言稿。

三、研讨评价

丁仁友校长：

1.创设情境，感受数学来源于生活，在交流思考中感悟数学；

2.鼓励学生用不同的方法探索，有助于学生理解“无理数”的概念；

3.学生表达语言完整清晰，教师引导的好，让生主动提问题，培养思考能力；

4.课堂活动多，操作体验丰富。

徐自钱主任：

1.丰教态自然大方，语言生动形象，评价语言丰富；

2.注重学生的自主提问，培养了学生主动学习的能力；

3.教学中通过思考、交流、动手操作，让学生体会到现实生活中存在的“无理数”，引导到位。

四、教学设计

有理数与无理数

【学情分析】

《有理数与无理数》是苏教版初中数学七年级第二单元有理数的第二节。学生在小学阶段已对数有了初步的认识，主要是自然数，正小数，正分数，进入初中接触到了负数，学生对数的认识有了进一步的扩充，同时也知道了可以把学到的数划分为整数和分数，从而把数扩充到有理数的范围。学生具备了主动参与、合作交流的意识和初步的观察、分析能力，而且在已经学习了有理数的基础上，学生通过自主探究等活动能以积极的态度投入到本节的学习中来。

【教学目标】

1．使学生理解有理数、无理数的意义，并能将给出的有理数进行分类；

2．培养学生树立分类讨论的思想。

【教学重点】 正确理解有理数与无理数的概念。
【教学难点】 对数进行分类。
【教学具准备】多媒体课件。
【教学过程】

（一）自主学习

师：我们上了六年多的数学课,学过不计其数的数,概括起来我们都学过哪些数呢?

生：在小学我们学过自然数、小数、分数.在前面几节课我们还学习了负数。

师：我们在小学学的是非负数，在初一发现数不够用了，于是便引入了负数，即把从小学学过的正数、零扩充了范围。你们能够用所学的知识完成下面的表格吗？请各位动手试一试。（1分钟）

判断下表中的各数分别属于哪一类？（在空格里打“√”）（5分钟）

师：下面，请一位同学与大家分享一下它的结果。（3分钟）

生：                                                              

师：你为什么认为0.25 是分数呢？

生：因为它就是1/4，当然是分数啦。

师：这个题目告诉我们，分数与小数可以互相转化。

（二）新知探究

思考：整数、小数、分数之间有有着怎样的联系呢？我们来做一个游戏：

有一篮子装有8个苹果，现在给两个小朋友分，每人几个？如果给3个小朋友分，每人几个？如果给4个小朋友分，每人几个？5个？6个？7个？8个？同学们动手算一算？

（师生一起进行运算，并将运算结果写在黑板上）

师：通过计算，我们有什么发现？

生：分数可以表示整数，有限小数和循环小数。

师：反过来，这些有限小数和循环小数及整数都可以化为分数的形式，例如：5=5/1、-4=-4/1 、 0.2=1/5 、0.618=618/100、0.3333……=1/3、0.2666……=4/15我们把能够写成分数（m、n是整数，n≠0）”形式的数称为有理数。

师：整数和分数统称为有理数。现在我们认识了有理数，按照有理数的定义，我们可以将有理数进行分类,如：

                     正整数

整数      0        

                     负整数

有理数                正分数  

 分数

                    负分数

师：我们认识了有理数，并且会将有理数进行分类，你们会把小数进行分类吗？试一试？

             有限小数     —— 有理数

小数

                      无限循环小数 —— 有理数

             无限小数

                          无限不循环小数 —— 有理数 ？

（三）合作、探究、展示

师：整数和分数统称为有理数，那么是不是所有的数都是有理数呢？这个问题古人也进行了研究，伟大的古希腊数学家毕达哥拉斯认为所有的数都是有理数，因为它们都可以写成分数（m、n是整数，n≠0）的形式。但是他的一个学生希帕索斯在研究中发现有些数不能写成分数的形式。它们是一些什么样的数呢？我们一起来研究研究。

1.做一做：

有两个边长为1的小正方形，剪一剪，拼一拼，设法得到一个大正方形。

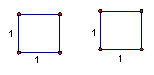
（让学生动手做一做，并请一位同学讲拼好的图形张贴在黑板上）

师：你知道这个大正方形的面积是多少吗？

生：2

2.想一想：

师：你知道这个正方形的边长是多少吗？

生：不知道。

师：你能求出它的边长吗？

设大正方形的边长为a，a满足什么条件？

生： a2=2

师：a可能是整数吗？说说你的理由

生：不可能，因为12=1，22=4，32=9，...越来越大。而a2=2，所以a不可能是整数。

师：a可能是分数吗？说说你的理由

生：不可能。（学生可能不会说理由，此时可师生共同探索）

师：因为… 两个相同分数因数的乘积都为分数。又因为a2大于1且a2小于4，所以a大致为1点几，即可判断出a 是大于1且小于2的数。（选取无限多大于1且小于2的两个相同分数的乘积来考查。体会“无限”的过程，认可找不到一个数的平方等于2，即a 也不可能是分数）在等式a2=2中，a既不是整数，也不是分数，也就是不能写成 的形式，所以a不是有理数。

3.算一算：

师：我们知道a肯定比1大而比2小，可以表示为1＜a＜2.那么a究竟是1点几呢？请大家用计算器进行探索，首先确定十分位，十分位究竟是几呢？如1.12=1.21，1.22=1.44，1.32=1.69，1.42=1.96，1.52=2.25，而a2=2，故a应比1.4大且比1.5小，可以写成1.4＜a＜1.5，所以a是1点4几，即十分位上是4，请大家用同样的方法确定百分位、千分位上的数字.

（师生共同用计算机进行计算,让学生体会无限逼近的数学思想）

a=1.41421356…，还可以再继续进行，且a是一个无限不循环小数.

（2）请大家用上面的方法估计面积为3的正方形的边长b的值.边长b会不会算到某一位时，它的平方恰好等于3？请大家分组合作后回答.

b=1.732051…，还可以再继续进行，b也是一个无限不循环小数.

师：其实，在很久以前，我们已经接触过限不循环小数，你们知道是什么吗？

生：圆周率π=3.14159265…也是一个无限不循环小数

4、无理数的定义：

我们把这一类的新数，即                                   的小数叫做无理数。

5、有理数与无理数的主要区别:

(1)无理数是无限不循环小数，有理数是有限小数或无限循环小数.

(2)任何一个有理数都可以化为分数的形式，而无理数则不能.

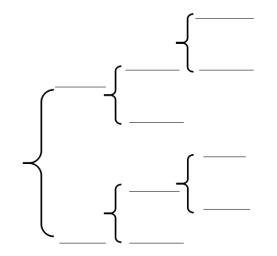
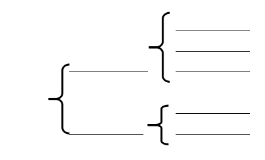6、数的分类:(学生独立完成)

①按定义分：    

②按照正负数分：

（四）例题讲解

例1.学习了有理数和无理数两个概念后，下面几个数，它是有理数，还是无理数？

－3、1.1414、2π、0.1010010001…、－0.1010010001…、、3.1415926．

例2.    把下列各数填在相应集合内：，-π

  正有理数集合：

｛                                                        ，…｝

  负无理数集合：

｛                                                       ，…｝

  非正整数集合：｛                                           ，…｝

     非负分数集合：｛                                           ，…｝                                    

例3.你还能写出一个无理数吗？

（五）巩固练习

1.判断题. (1)无理数都是无限小数. （    ）        

   (2)无限小数都是无理数. （    ）

(3)有理数与无理数的差都是有理数.  （    ）

(4)两个无理数的和是无理数.      （    ）  

2.把下列各数填在相应的大括号内：，0，，3.14，－，，，－0.55，8，1.121 221 222 1…(相邻两个１之间依次多一个２)，0.211 1，999

正数集合：｛               …｝；

负数集合：｛               …｝；

有理数集合：｛                …｝；

无理数集合：｛                     …}.

3.以下各正方形的边长是无理数的是（ ）

（A）面积为25的正方形；(B)面积为16的正方形；(C)面积为3的正方形；(D)面积为1.44的正方形.

（六）课堂小结

1．什么叫无理数？

2．数的分类？

3．如何判定一个数是无理数还是有理数.

（七）布置作业

   课本P17 练一练 ，习题2.2

【板书设计】

五、教学反思

有理数与无理数教后反思

学生在小学阶段已对数有了初步的认识，主要是自然数，正小数，正分数，进入初中接触到了负数，学生对数的认识有了进一步的扩充，同时也知道了可以把学到的数划分为整数和分数，从而把数扩充到有理数的范围。学生具备了主动参与、合作交流的意识和初步的观察、分析能力，而且在已经学习了有理数的基础上，学生通过自主探究等活动能以积极的态度投入到本节的学习中来。

通过学生动手操作去发现数不够用了，而不是直接把概念呈现给学生，使学生更深地体会“数学来源于生活，服务于生活”的道理，很真实、很自然。使学生从“感兴趣”自然进入数学知识的探究，达到培养思维能力的培养。“授之以鱼，不如授之以渔”，这才是素质教育的真正目标。教学过程中注重培养学生探究能力的培养，还课堂给学生，让学生亲身体验知识发生的过程，拓展学生的创造性思维。同时，注意加强对学生的启发和引导，鼓励培养学生的大胆猜想。最后从整个课堂效果来看，这节课始终围绕教学目标展开，层次比较清楚，环节紧凑，并注意引导学生通过观察、分析、动手实践、自主探索、合作交流等活动，突出体现了学生对知识的获取和能力的培养。

六、活动照片

七、活动签到表